馬好きエンジニアです。
皆さんは競馬予想の際に軸は「人気馬 or 穴馬」のどちらが多いですか?
自分は人気馬を軸にすることが多くて、 2・3番人気の馬からワイドで中穴に流すことが多いです。
どちらかというと軸には人気馬を選ぶ人のほうが多いのではないでしょうか。
そこで今回の記事では「1~3番人気の人気馬」がどれくらいの確率で馬券圏内に来ているのか過去のレースデータを分析して紹介したいと思います!
人気馬が馬券圏内に来る確率が分かれば、効率的にレース選択をすることができ、高配当馬券の的中率を上げることができます。
- 馬券圏内に来る確率=複勝率
- 1番人気が馬券圏内に来る確率:64%
- 2番人気が馬券圏内に来る確率:51%
- 3番人気が馬券圏内に来る確率:41%
どうやって分析するの?
まず初めに馬券圏内に来る確率を定義させてください。
「馬券圏内に来る確率 = 複勝率」
今後馬券圏内に来る確率というワードがでたら上記のように解釈してください!
では分析手法の説明に入っていきます!!
分析には「着順ごとの頭数を累計した値」を各人気において利用します。
文章だけでは??だと思うので、もう少し嚙み砕いて説明していきますね。
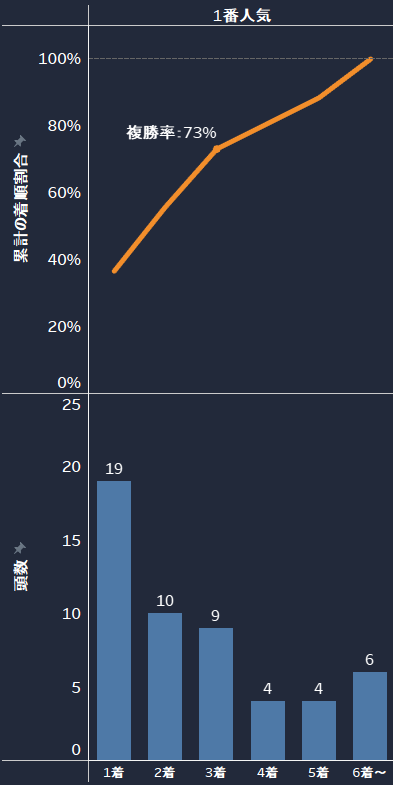
例えば、「東京 芝 2000m 良 2勝クラス」における1番人気の馬券圏内に来る確率を求めるとしましょう。このとき、着順ごとの頭数を累計した値から確率を求めると73%という結果になりました。
10頭走ったら7頭は馬券圏内に来る。かなり高い数値ですね。それではこの値をどのように求めたか見ていきましょう。
① 対象となる競走馬の全頭数を求める
下段の棒グラフより、今回の条件で対象となった競走馬の頭数は全部で52頭になります。
| 競走馬の頭数 | 19+10+9+4+4+6=52頭 |
② 着順ごとの累計値を求める
着順ごとに競走馬の累計値を求めます。これは単純に該当着順以上の頭数を足し合わせればOKです。
※「6着~」は6着以降の頭数をまとめて表示しています。
| 1着の頭数 | 19頭 |
| 1~2着までの頭数 | 19+10=29頭 |
| 1~3着までの頭数 | 19+10+9=38頭 |
| 1~4着までの頭数 | 19+10+9+4=42頭 |
| 1~5着までの頭数 | 19+10+9+4+4=46頭 |
| 5着まで+6着~の頭数 | 19+10+9+4+4+6=52頭 |
このとき、「5着まで+6着~の頭数を累計した値」と競走馬の頭数は一致します。
③ 着順ごとの累計値を全頭数で割る
最後に着順ごとの累計値を全頭数で割ると、各着順までに来る競走馬の割合を求めることができます。
| 1着に来た割合 | 19÷52=0.37 37% |
| 2着までに来た割合 | 29÷52=0.56 56% |
| 3着までに来た割合 | 38÷52=0.73 73% |
| 4着までに来た割合 | 42÷52=0.81 81% |
| 5着までに来た割合 | 46÷52=0.88 88% |
| 全着順に来た割合 | 52÷52=1.00 100% |
馬券圏内に来る確率=複勝率なので、この場合だと3着までに来る割合である73%が求める値となります。
以上が馬券圏内に来る確率の求め方となります。この方法でレース条件を指定するなどして高配当レースを探していきます。
1~3番人気が馬券圏内に来る確率
高配当レースを見つけるためには基準となる確率の値が必要です。比較することで対象のレース条件は荒れやすいのか固いのか判断することができます。
そこで次に、競馬場・クラス・距離・芝ダ・馬場など問わない全レース条件における1~3番人気が馬券圏内に来る確率を表示します。
この値を基準とすることで、レース条件を指定した際の分析で高配当レースなのか判断することができます。
| 1番人気の3着内率 | 64% |
| 2番人気の3着内率 | 51% |
| 3番人気の3着内率 | 41% |
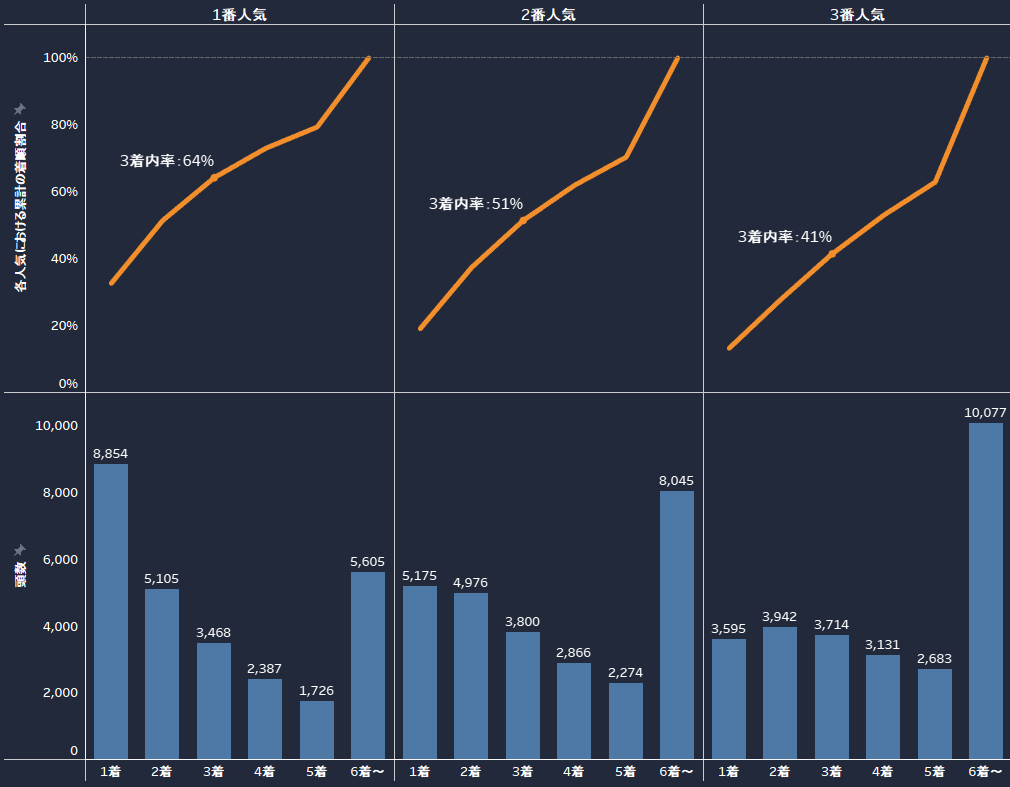
※集計期間:2015/1/1~2023/2/26
レース条件を指定しないで1~3番人気の3着内率を求めると、1番人気 ⇒ 64%、2番人気 ⇒ 51%、3番人気 ⇒ 41%という結果になりました。
個人的な印象として1番人気が5回に3回は馬券圏内に来る確率なので、馬券的中を狙ううえでは軸としてまず考えるのが賢明かなと思いました。
まとめ
今回は「人気馬がどのくらいの確率で馬券圏内に来るのか?」というテーマでした。
皆さんは分析結果を見てどのような印象を持ちましたでしょうか。
今回紹介した分析手法から各レース条件の値を求めることで、高配当レースなのか判断することができます。
そこの見極め方については、また次回以降で詳しく解説していきたいと思いますので乞うご期待!
それではまた次回もよろしくお願いします!